S.P. Rajaguru¹, C.R. Sangeetha², and Durgesh Tripathi²
1. Indian Institute of Astrophysics, Bangalore-34, India
2. Inter-University Centre for Astronomy and Astrophysics, Post Bag-4, Ganeshkhind, Pune 411007, India

The Sun and sun-like stars require a constant source of basal flux of energy to heat their chromospheres and to balance the observed radiative losses. For the quiet Sun, the required energy flux is ~4.6 kW m^-2 at the lower chromospheric heights. Charting out the sources of such energy supply is a long-standing problem in solar physics.

A favored mechanism has been the heating by acoustic waves that can propagate up, hence of frequencies larger than the photospheric acoustic cut-off ν of ~5.2 mHz. However, observational estimates backed by numerical simulations showed that such waves carry only about one-tenth of the required energy^[1], raising the possibility that the photospherically anchored small-scale magnetic fields could play a dominant role. Since then, waves of different nature, viz. acoustic, magneto-acoustic, and Alfvén type, with periods in the 5 minute range corresponding to the Sun’s internal p modes, have been ubiquitously observed in the solar atmosphere. This has largely been attributed to inclined magnetic fields that can lower the cut-off frequency. In a study^[2] published recently, however, we report the detection of a significant fraction of such waves originating in the nearly vertical magnetic field elements of the quiet-Sun defying the above explanations.

Figure 1| Maps of magnetic inclination angle θ (bottom panel), phase travel time, and logarithm of energy flux over the quiet-network area for acoustic waves of frequency 3 mHz propagating from 170 km (HMI line-core intensity I_co) to 360 km (AIA 1700Å).

Exploiting simultaneous photospheric vector magnetic field, Doppler, continuum, and line-core intensity (of FeI 6173Å) observations from SDO/HMI and lower-atmospheric UV emissions in the 1700Å and 1600Å channels of the SDO/AIA, we have studied in detail the relationships between magnetic inclination and strength and the acoustic wave propagation (phase travel time) over quiet, plage, and sunspot areas (see Ref. [2] for details). We show in Figure 1 the 3 mHz maps of phase travel-times and energy fluxes, along with that of magnetic inclination, θ, to the solar surface normal, over a quiet-Sun area. It is clear that the energy fluxes concentrate within the discrete magnetic field elements, confirming the presence of magneto-acoustic portals[3]. From the maps in Figure 1, we derive 2D functions shown in Figure 2. We have over-plotted the theoretical minimum due to magnetic fields in the maps of Figure 2. The region of smaller θ and ν bounded by this curve in the θ-ν plane, in principle, is not accessible for wave-propagation via reduction in ν_ac due to θ. However, strikingly, almost the whole of this region of low ν and θ<60° is filled with propagating waves in the case of lower height (360 km, 1700Å). Thus the relatively less-inclined, nearly vertical magnetic field elements in the quiet-Sun channel a significant amount of acoustic waves of frequencies, in the range of 2 - 4 mHz.

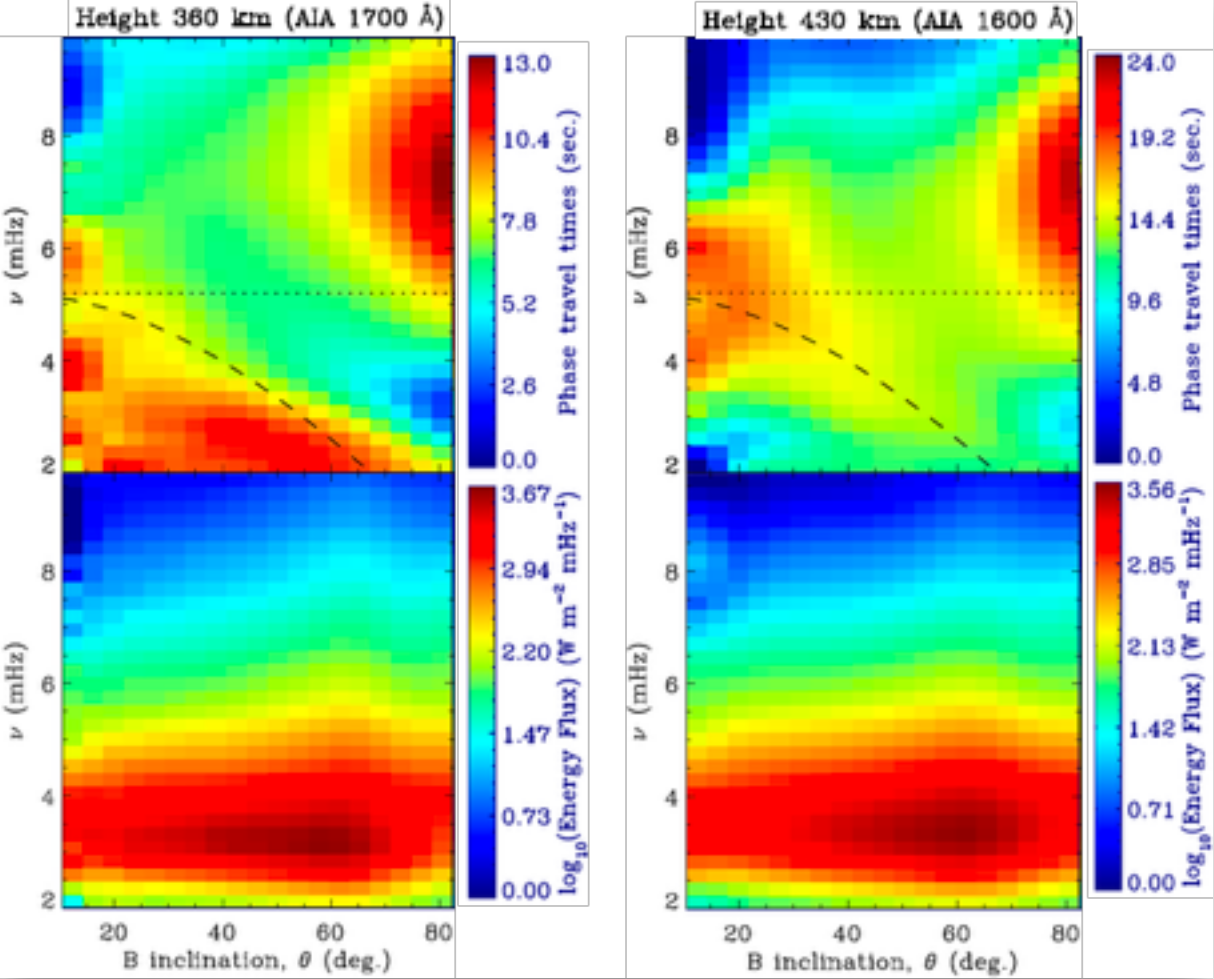Figure 2| Phase travel times and logarithm of energy fluxes against θ and wave frequency, ν, over the quiet-Sun regions; left panels are for AIA 1700Å height (360 km) and the right panels are for AIA 1600Å height (430 km). The dotted line in each panel is the cutoff frequency ν_ac=5.2 mHz, and the dashed line is ν_ac cosθ.

The mean energy flux over the quiet-Sun (or quiet magnetic network), over the 2 – 5 mHz frequency region, between the upper photosphere and heights corresponding to AIA 1700Å and 1600Å intensities is in the range of 2.25 to 2.6 kW m^-2 (Figure 3), which is about twice the previous estimates^[3]. Out of this total quiet-Sun acoustic flux, about 25 to 30% is due to the above identified wave-propagation in the 2 – 4 mHz over the vertical magnetic fields.

Figure 3| Mean wave-energy fluxes against frequency at heights 360 km (AIA 1700~{\AA}). The three curves, black, red and pink correspond to mean fluxes over quiet-network, plage and spot areas, respectively. Frequency-integrated fluxes over 2 – 5.2 mHz and 5.2 – 10 mHz ranges are marked.

As discussed in detail in our paper^[2], we find that the case of the tube mode (or sausage mode) subject to strong photospheric radiative damping, as theorized by Roberts^[4], provides an interesting explanation for our results for quiet-Sun magnetic fields. An alternative possibility is the magneto-convective process^[5] within flux tubes or sheaths that drive upward propagating longitudinal waves over a broad frequency range, 1 – 10 mHz, with peak power around 4 mHz, providing possible explanations for our observational results in Figures 2 for the quiet-network.

Please refer to Ref. [2] for details.

References

[1] Fossum, A., & Carlsson, M. 2005, Nature, 435, 919
[2] Rajaguru, S. P., Sangeetha, C. R., & Tripathi, D. 2019, ApJ, 871, 155
[3] Jefferies, S. M., McIntosh, S. W., Armstrong, J. D., et al. 2006, ApJL, 648, L151
[4] Roberts, B. 1983, Solar Phys, 87, 77
[5] Kato, Y., Steiner, O., Hansteen, V., et al. 2016, ApJ, 827, 7